The Space Place Experiment center will help you conduct real life science experiments and learn how the world works. Whether you were sent here by your teacher or you found this on your own, you're going to have some fun!
Get an adult involved in any Space Place experiment! These experiments aren't dangerous but they could make a mess.
What type of experiment would you like to do?
Welcome Back!
What's your case number?
log in Try Another ExperimentOops! Ok. We'll try to help.
If you haven't started an experiment at all yet, go back and choose an experiment.
If you've already started we might be able to help if you access this page from the same computer you began the experiment on.
Identity Lookup
Does [this | any of these] look like your experiment?
Are none of these yours? We can't do anything else to help. You'll have to start again. Write down your case number!
Water Experiment
You have selected the moisture experiment. Here, you will have the opportunity to grow your own lima bean plant. A bean is simply a very large seed. The purpose of this experiment is to see what effect moisture has on a bean’s ability to grow into a plant. To continue the experiment, please make sure you have the following items ready:
- 3 Lima Beans
- 3 Ziplock Sandwich Bags
- 15 Cotton Balls
- A measuring spoon
- Tape (scotch, packaging, duct)
- Water
Once you have these items, please press continue.
continue Try Another ExperimentYour lookup code is:
123456Please write this down! If you don't write it down you won't be able to continue your experiment later!
OkayI wrote it down. I promise.
Day One
Please follow these steps carefully:
- Fill each bag with 5 cotton balls and one lima bean.
- Label each bag with a number (1, 2, and 3).
- Add 1 tablespoon of water into the first bag.
- Add 5 tablespoons of water into the second bag.
- Add 12 tablespoons of water into the third bag.
- Seal the bags.
- Tape the bags to a window that receives plenty of sunlight.
Hypothesis:
-
Do you think the amount of water in each bag will have an effect on how much the beans grow? Why?
saveDo you think all of the lima beans will grow? Explain your answer.
saveWhich lima bean do you think will grow the most? Why?
saveWhich lima bean do you think will grow the least? Why?
saveAdd any observations you might have:
save
What do they look like?
Choose an image that looks like each plant! It's OK if they all look the same so far!

Plant 1

Plant 2

Plant 3
Pick the image that most matches the shape of your plant.
Day N
Choose an image that looks like each plant! It's OK if they still look the same!

Plant 1

Plant 2

Plant 3
Pick the image that most matches the shape of your plant.
Add any observations you might have:
saveFinal Observations
You've been running the experiment for 5 days. We recommend running this experiment for at least 8.
Back to ExperimentDid water affect how much the beans grew?
saveDid all of the lima beans grow?
saveWhich lima bean grew the most?
saveWhich lima bean grew the least?
saveWhy do plants need water?

Plants are thirsty. They need water to create food. Plants create their own food in a process called photosynthesis. This process uses the energy from light to combine carbon dioxide (from the air) and water (from the ground) to produce sugar. They use the sugar as food.
Without enough water, there would be no photosynthesis, and plants would be unable to survive. Too much water, though, and the plant will drown. Too much water can block the air from reaching the plant and can cause it to rot.
The amount of water in the soil partly determines how much a plant will grow. This means that water also partly determines how much carbon dioxide plants take in from the air.
Scientists are very interested in figuring out how much carbon dioxide plants take in across different areas because carbon dioxide causes our planet to warm. To figure this out, they need to know how much water is in the soil in different areas—a hard measurement to come by.
NASA has come up with a solution to this problem. Two missions—AirMOSS and UAVSAR—can study soil moisture from the sky. Both AirMOSS and UAVSAR are special kinds of radar attached to a plane. Scientists can measure how much moisture is in the soil that AirMOSS or UAVSAR flies over. AirMOSS can actually measure how much moisture is in the part of the soil that the plant’s roots are in.
Using this information, scientists may be able to figure out just how much carbon plants take in over all of North America!
Light Experiment
You have selected the light experiment. Here, you will have the opportunity to grow your own lima bean plants. A bean is simply a very large seed. The purpose of this experiment is to see what effect light has on a bean as it grows into a plant. To continue the experiment, please make sure you have the following items ready:
- 8 Lima Beans
- 4 toilet paper rolls
- Strips of ripped newspaper
- Potting soil
- A measuring spoon
- 2 trays or plates
- Water
Once you have these items, please press continue.
continue Try Another ExperimentYour lookup code is:
123456Please write this down! If you don't write it down you won't be able to continue your experiment later!
OkayI wrote it down. I promise.
Day One
Note: This experiment suggests that you plant 8 beans (four in the light and four in the dark). This is to make sure you have at least one bean sprout in each group—it's not 100% guaranteed that each bean will sprout. As the experiment progresses, you should record the results from only one plant in each group and stick with that plant for the whole experiment. You should pick the plant that is growing the most.
Note: It may take up to a week to see any plants sprout. Please run the experiment for at least two full weeks.
Please follow these steps carefully:
- Cut the toilet paper rolls in half so that you have 8 small cylinders (ask a parent or older sibling to help with this step!)
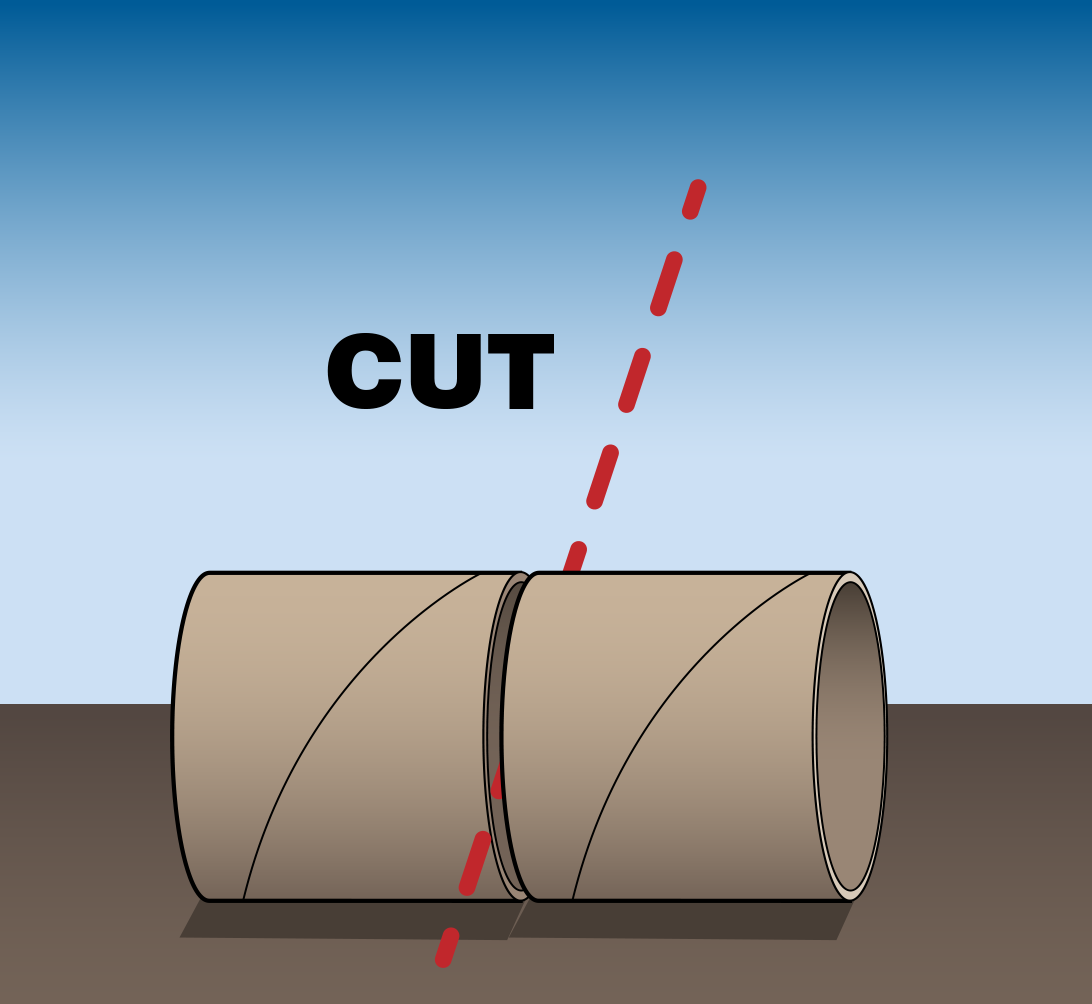
- Coat the inside of each cylinder with newspaper strips so that the bottom can hold potting soil.

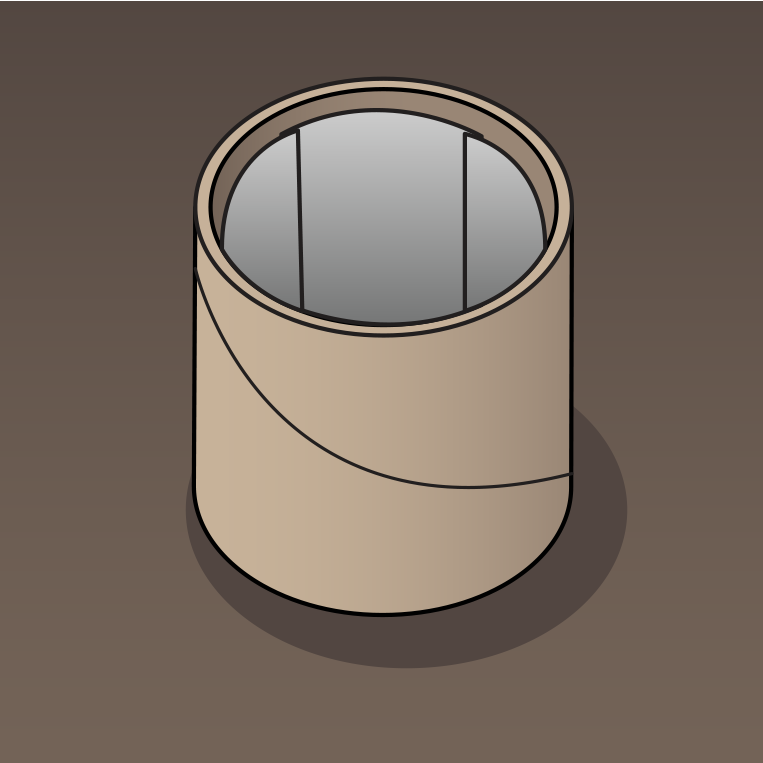
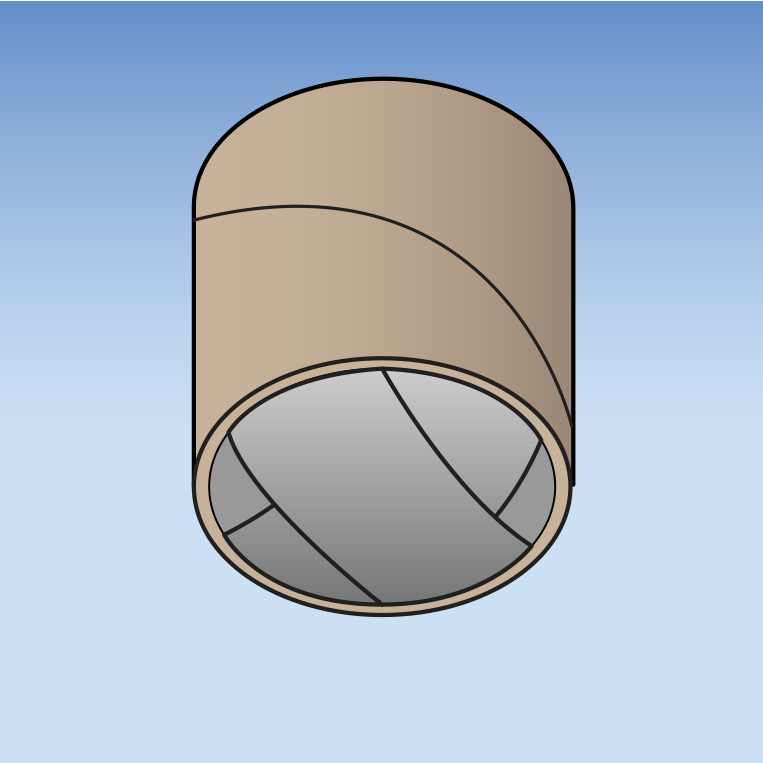
- Fill each cylinder with enough dirt so that you leave only about 1/4 inch of cardboard showing at its top.
- Make a small hole no deeper than an inch and no wider than your thumb in the potting soil in each cylinder.
- Place one lima bean in each hole and cover it completely.
- Place 4 cylinders on one tray or plate, and 4 on the other.
- Water all 8 by putting 2 tablespoons of water in each.
- Take one tray of 4 cylinders and put it in a spot that will be pitch black all day every day.
- Take the other tray and leave it in a place that receives plenty of sunlight during the day.
- When you are done with the experiment, you can leave your plant in the cardboard cylinder and place it right in a plant pot or garden!
Hypothesis:
-
Do you think the amount of light the two groups of plants get will have an effect on the beans as they begin to grow? Why?
saveWhat do you think will happen to the lima beans that receive sunlight? Explain your answer.
saveWhat do you think will happen to the lima beans that do not receive sunlight? Explain your answer.
saveAdd any observations you might have:
save
What do they look like?
Choose an image that looks like one plant from each group. It's OK if they all look the same so far, but when they begin to sprout you should pick the plant that is growing the most and record only that plant for the rest of the experiment.
Plant 1

Plant 2
Pick the drawing that most closely matches your plant.
Day N
Choose an image that looks like the one plant you have selected from each group! It's OK if they all look the same in the beginning!

Plant 1

Plant 2
Pick the drawing that most closely matches your plant.
Add any observations you might have:
saveFinal Observations
You've been running the experiment for 5 days. We recommend running this experiment for at least 14.
Back to ExperimentDid the amount of light the two groups of plants received have an effect on the beans? If yes, what was that effect?
saveDescribe what happened to the lima beans that received sunlight.
saveDescribe what happened to the lima beans that received no sunlight.
saveWhat’s going on here?
When your bean plants first sprouted, they could grow without creating their own food because they had plenty of food stored away in the bean. Later, when they run out of this food, they need to create their own.
Plants use the energy from light to convert water (from the ground) and carbon dioxide (from the soil) into sugar. This sugar is their food.
To use the energy from light, they need a special chemical called chlorophyll. Chlorophyll is like a natural solar panel—it absorbs light and creates energy.
Chlorophyll is what gives plants their green color. A plant that is using the sun for photosynthesis is green because it is using a lot of chlorophyll.
If a plant grows without sunlight, it does not use chlorophyll. The plant you grew without light is white because it never created any chlorophyll. It wouldn’t have made sense since there was no light to be found anyway and there was still plenty of food in the bean.
Light comes in many different colors depending on its wavelength. Chlorophyll absorbs all of these colors except for the green wavelengths. This means that the green is reflected back to your eye. This is what gives chlorophyll, and plants in general, a green color.
Plants use their leaves to collect the energy from light. This is why the leaves were so much bigger on the plant that grew in the light. The plant grown in the dark did not have much of a use for them.
What do you think would happen to the plant grown in the dark if you kept growing it for a longer period of time? What do you think would happen if you brought it into the light?
That's it!
That's all you need to do for today. Come back soon and keep updating your science log!
Try Another ExperimentResults
More Info Try Another Experiment