How do we talk to machines?
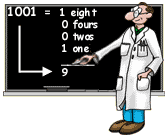
In our system of numbers, we normally use decimal notation. "Deci-" means 10. Decimal notation uses 10 digits:
0 1 2 3 4 5 6 7 8 9
The language we use to talk to machines is called binary notation. "Bi-" means two. Binary notation uses only two digits:
0 1
The rest of the information carried in a binary message depends on the position of the 0's and 1's. This is similar to decimal notation.
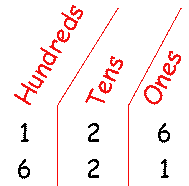
In decimal notation, for example, we know there's a big difference between the numbers 126 and 621. How do we know this? Because the digits (that is, the 6, the 2, and the 1) are in different positions. These positions are often called "place value positions."
It works the same way with binary numbers, except for one thing. To figure out how much each place value position is worth, you multiply by 2 (instead of 10) each time you move one more position to the left. So, here's how you would read the binary number 10110101:

How would you read these binary numbers?
1111
11110000
10010101
10101010